Davinsy, our autonomous machine learning system, integrates at its core Deeplomath, a deep learning kernel continuously learning from real-time incoming data. This paper describes the spiking nature of convolution function networks of Deeplomath.
Predefined network architecture and backpropagation
Let us recall the main characteristics of the state of the art in deep convolutional and recursive neural networks:
- The need for an a priori definition of the architecture of the network (number and types of layers, neuronal density, etc.) before the identification of the parameters via the solution of an optimization problem by back-propagation minimizing the learning error between the model and a database, while controlling the validation error.
- Beyond the architecture, the need to calibrate the hyper-parameters driving, in particular, the optimization phase.
- The need for a large database, not only to achieve a network giving good performance in inference, but also to be able, thanks to the richness of the data, to effectively recognize unknown situations. Otherwise, the model always provides an answer corresponding more or less to the closest scenario in the learning dataset. Obviously, this is not necessarily suitable as the closest can be still quite far and inadequate.
Adaptive real-time continuous learning
Deeplomath approaches the problem in a different way by removing the previous limitations that weigh on the deployment and use of deep networks in industrial applications:
- Encapsulate all the functionalities of the network layers within a single type of functional layer: the user no longer has to define the types of layer to be chained.
- Automatic identification of the depth of the network and the neural density by an original heuristic allowing joint identification of the parameters of the functions constituting the layers of our “function network”, thus avoiding the need for the solution of an optimization problem by back-propagation.
- Identification of the geometry of the contour of the “known set” allowing the rejection of ‘unknown’ scenarios without any a priori knowledge other than event-driven gathered information.
- Real-time reconstruction of the network, thanks to the low computational complexity of its heuristic, allowing adaptation to changes in the environment without the need for uploading to the cloud for learning.
Spiking networks
The previous construction leads to a network of function layers where the weights are not anymore constant values but functions that can vanishes making the network naturally spiking. We speak of functional synaptic coefficients.
The figure shows 3 inferences after training a database of dimension 2 to 43:
x(2) → y(43)
generated from solutions of a differential equation.
Outputs are time series and this is a multi-output regression problem.
At each inference less than 10% of the variables are active.
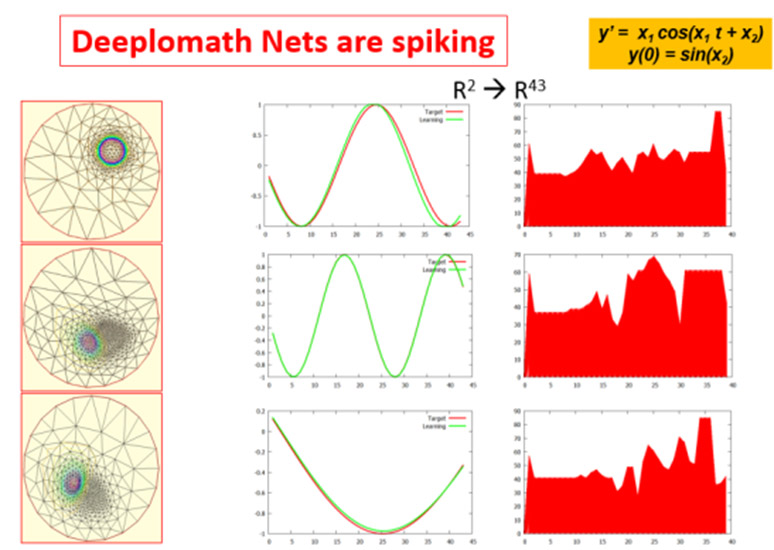
The pictures on the left show an analogy with spectral finite element meshes showing dynamic variable connection from one inference to the other.
The hyper-connected structure of Davinsy’s Deeplomath function network is mixed. In addition to communication between successive layers, the outputs of the network backscatter to all the layers (this is related to Lebesgue measures, making learning feeds back and forth) and all layers contribute to the outputs of the network.
A Convolution Function Network is a tensor of functions of rank 6 (>7 in open-set).

